

台風の風が左巻き(ひだりまき)なのはコリオリの力(ちから)のせいって聞いたよ。コリオリの力ってなに?

簡単(かんたん)に言えば、まっすぐに動いているものを曲げようとする見えない力のことだよ。

どうしてそんな力が働(はたら)くの?

地球の自転が関係しているんだ。
北半球では動いているものを右に曲げようとする力が働いて、南半球では左に曲げようとする力が働いているよ。
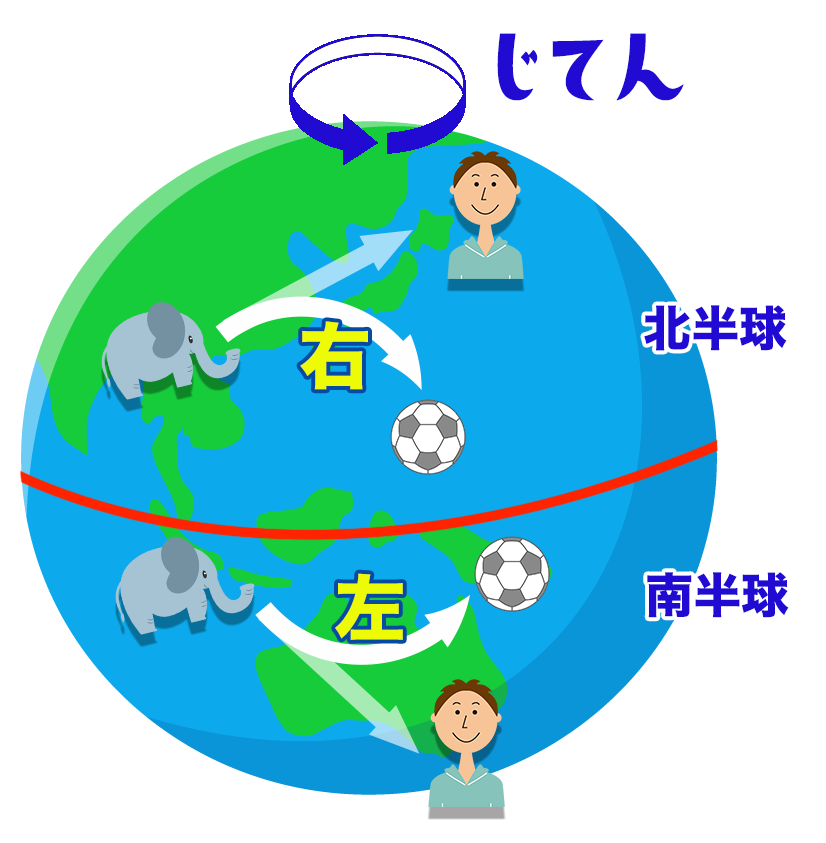

不思議(ふしぎ)だなぁ

ふつうの生活では感じないから分かりにくいよね。実験をしながら考えていこう。
ここに2つの「動く歩道」があって、それぞれゾウさんと僕が立っているとしよう。歩道は平行にならんで同じスピードで動いているよ。

ここでクイズその1。
ゾウさんが僕に向かってサッカーボールを投げたら、うまくキャッチできると思うかい?
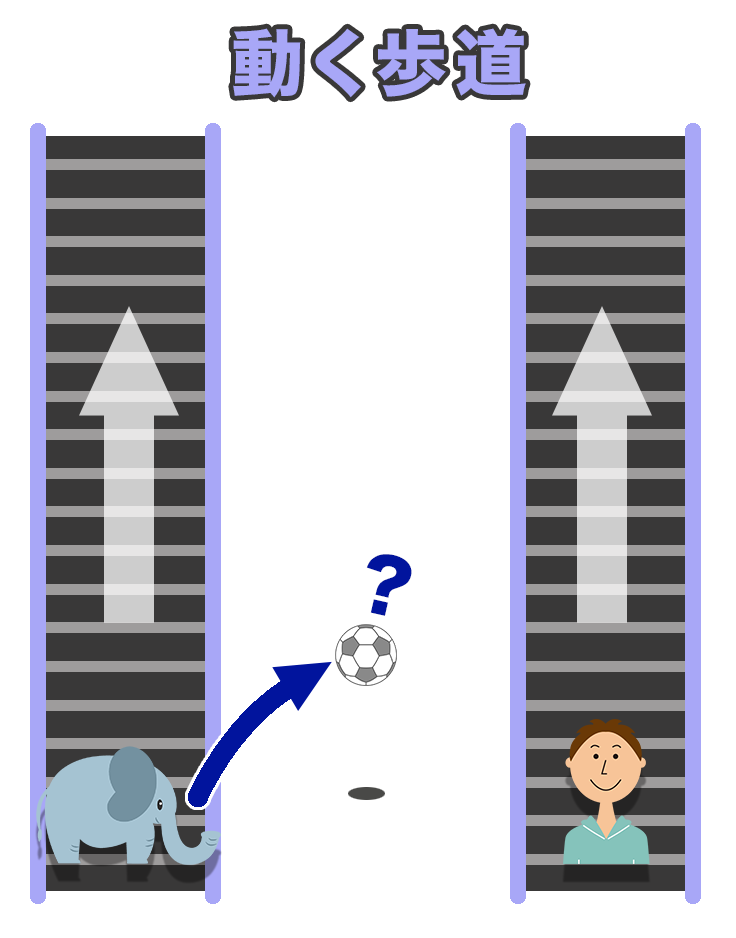

もちろんできるはず

そうだね。正解(せいかい)。
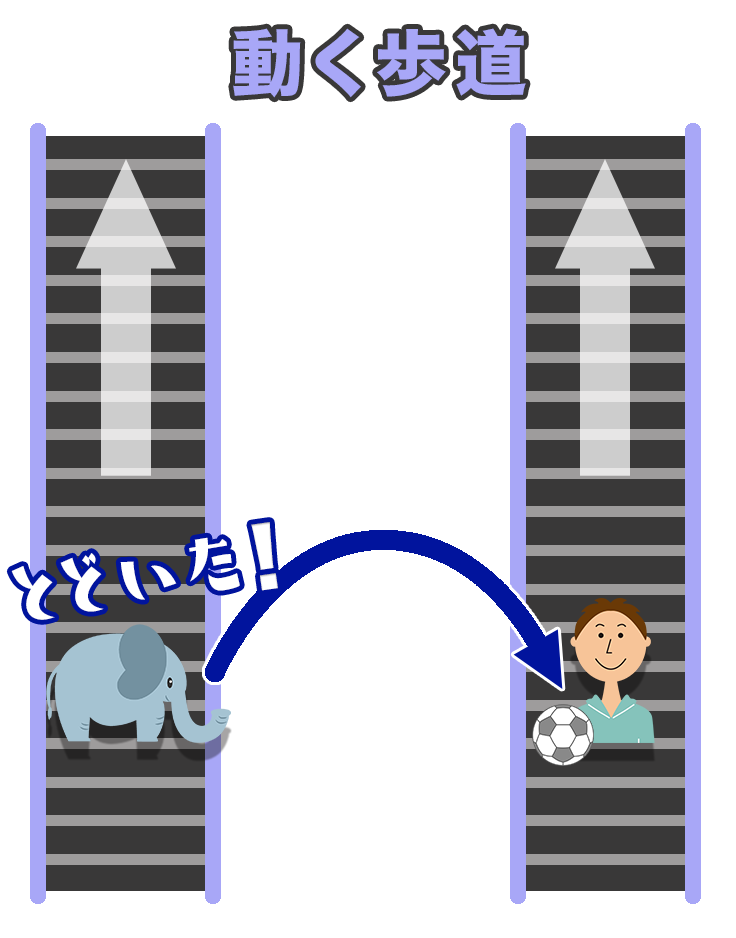
じゃあ、もし僕の歩道のスピードがゾウさんの歩道より速(はや)く動いていたらどうなると思う?
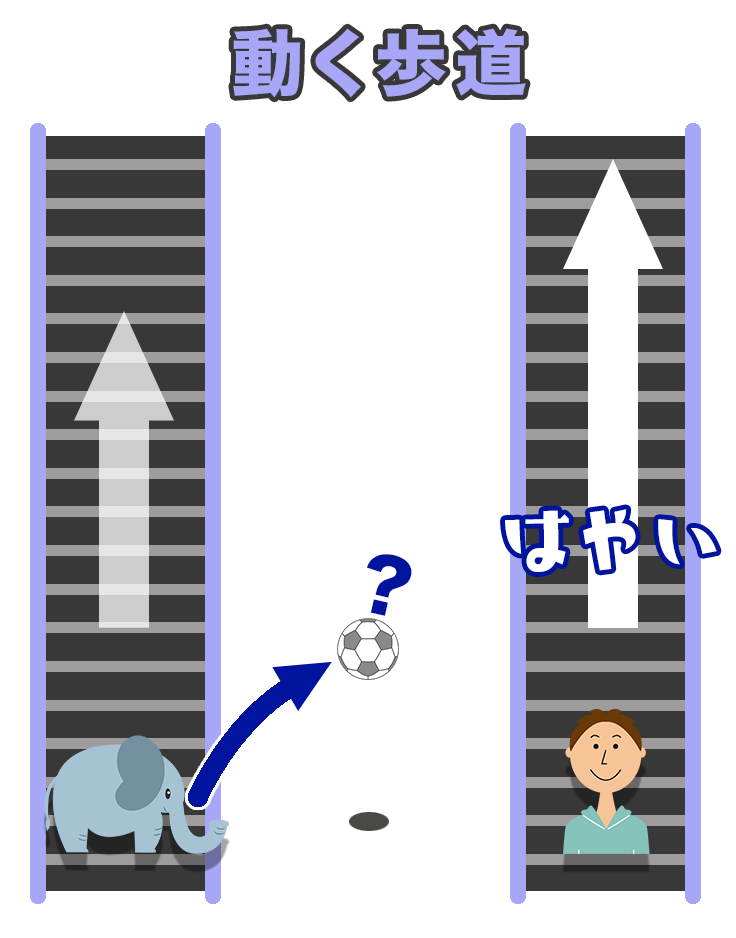

ボールがそっちに届(とど)くころには、そうた君は先に進んでいるかも

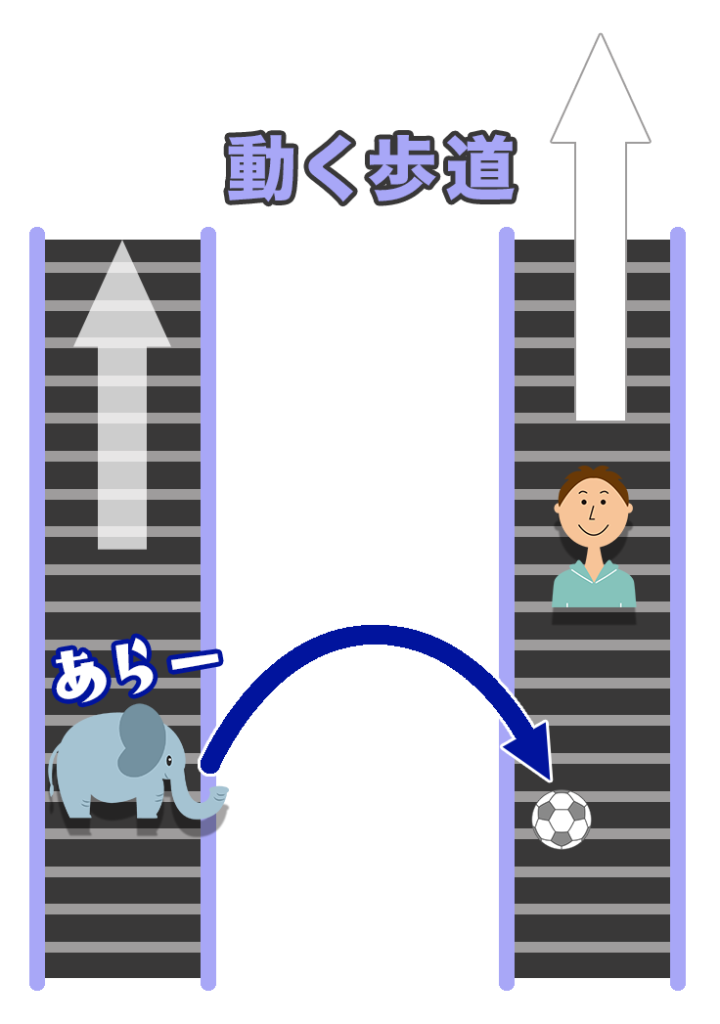
そうなんだ。
僕は速く進んじゃうからボールを受け取れず、うまくキャッチボールができないんだ。スピードの違(ちが)いのせいだね。
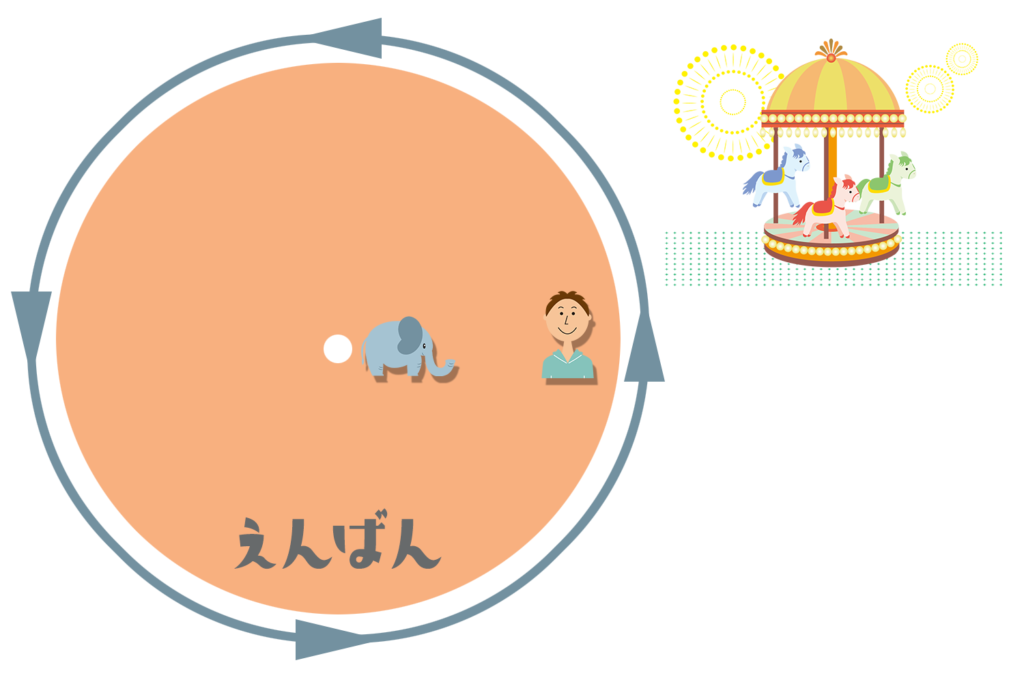
次に、左にぐるぐる回っている大きな円板(えんばん)の上でキャッチボールをしてみよう。
円板は遊園地にあるメリーゴーランドのような感じ。ゾウさんは中心の近くにいて、僕が外側(そとがわ)に立っているとするよ。
ここでクイズその2。
動く円板の上で、ゾウさんが僕に向かってサッカーボールを投げたら、ボールは僕に届(とど)くかな?円板が動いていることを想像(そうぞう)しながら考えてみよう。


うーん・・・
届くんじゃないかなぁ。

答えは「届かない」んだ。
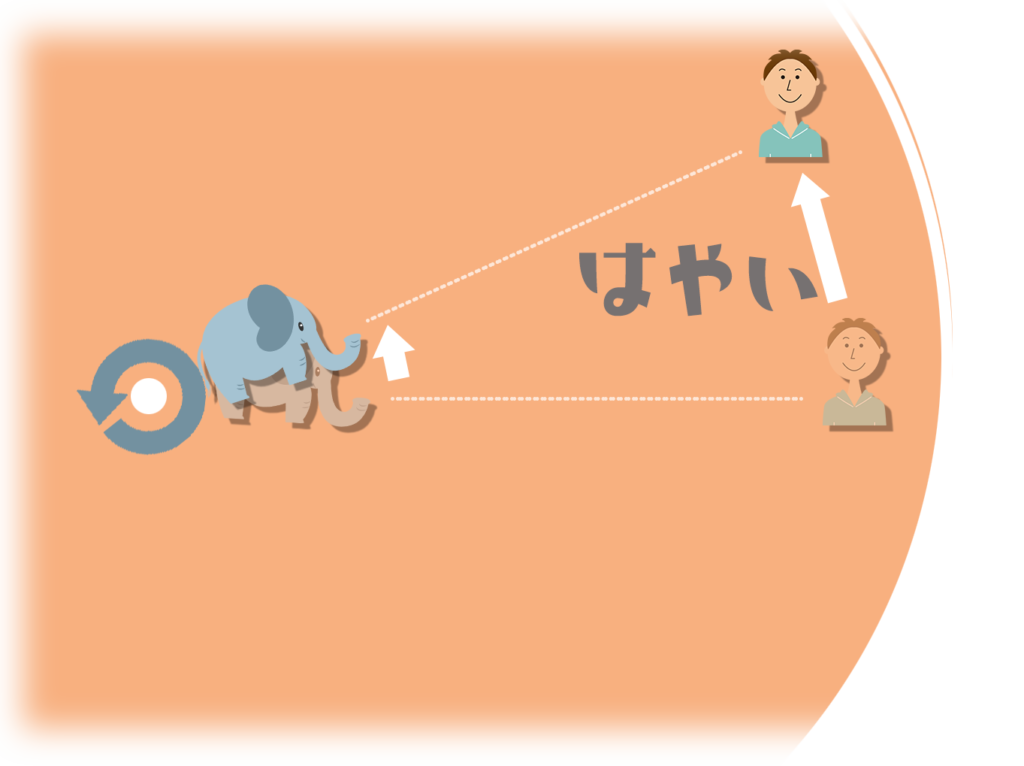
ボールが外側に届いた時には僕はそれより前のほうに進んでいるよ。

なぜかというと、回転する板の上ではゾウさんより外側にいる僕の方が動くスピードが速(はや)いからんだ。「動く歩道」の時と同じだね。

そっか。そう言われると分かるゾゥ

動く円板の上では、ゾウさんが僕に向かってまっすぐボールを投げても、ボールが届くころには僕は先に進んじゃっているんだ。最終的(さいしゅうてき)にボールはゾウさんから見て僕の右のほうにずれて落ちるよ。
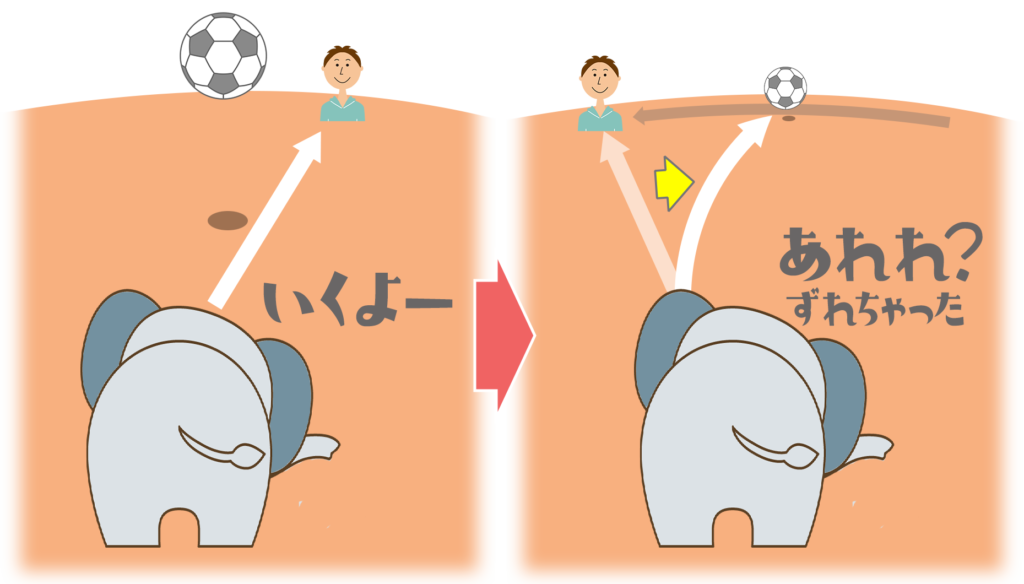

円板が動いていなかったらキャッチボールできたのになぁ

そうだね。
ここで円板の動きを地球の自転におきかえてみよう。右のイラストは北半球を北極(ほっきょく)の上から見たものだよ。円板と同じ左まわりに自転している。
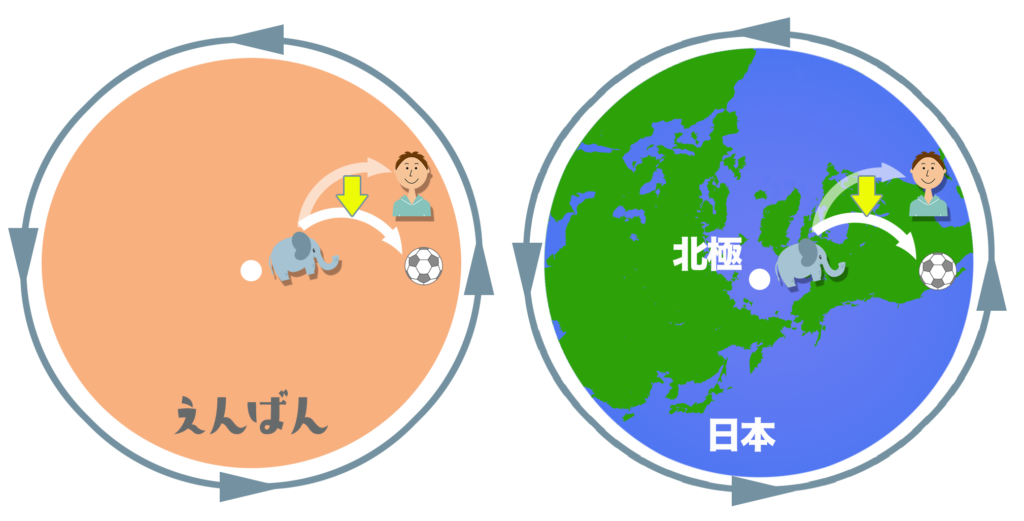
僕らが住んでいる北半球でキャッチボールをすると、円板の上でのキャッチボールと同じように、いつもボールはゾウさんから見て右にずれて届くんだ。

ええっ?
でも公園でキャッチボールするときはボールはまっすぐに飛んでいくよ

とても小さな変化(へんか)だから気づかないだけなんだ。
長い距離を飛ぶロケットみたいに動くスケールが大きいとはっきりしてくるよ。ロケットは飛びながら右にどんどんずれていくので、打ち上げる前に飛ばす方向をちゃんと計算するんだよ。この右にずれる力を「コリオリの力」というんだ。


へぇ。そうなんだね

今度は僕からゾウさんに向かってボールを投げてみよう。
「動く歩道」で僕のスピードが速い場合(ばあい)を考えてみるよ。
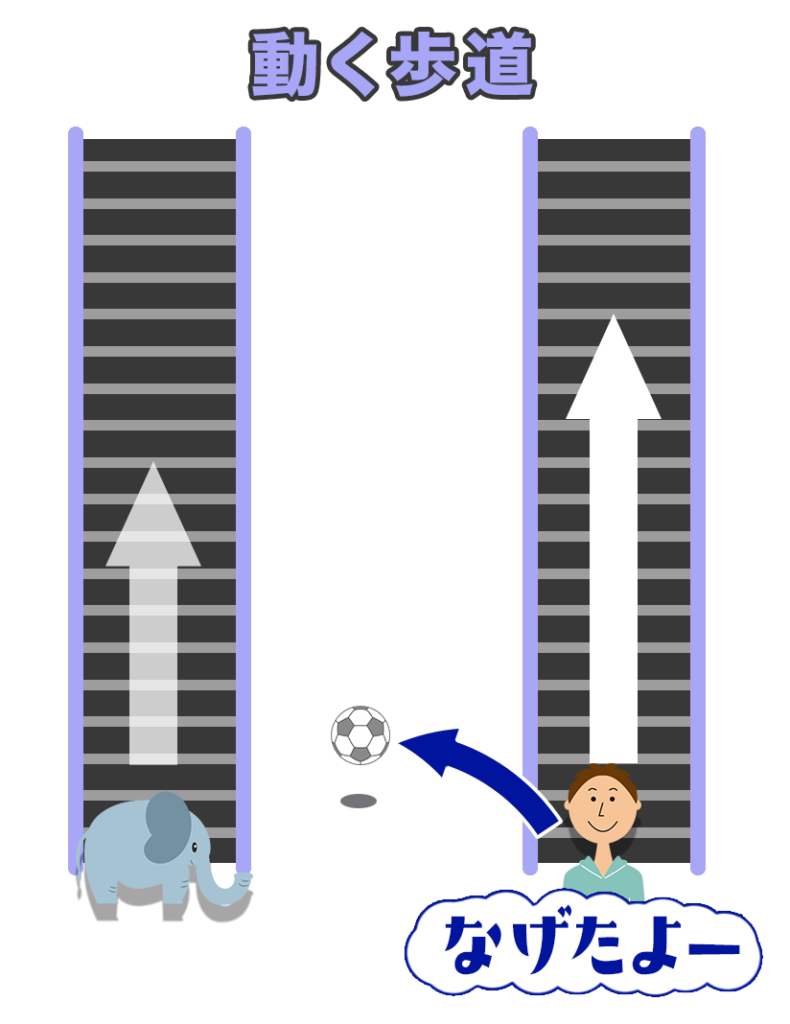
すると、ボールも速く飛んでゾウさんより先に歩道に届くよ。

それと同じように円板の上でも、ボールはゾウさんの前のほうに届くんだ。
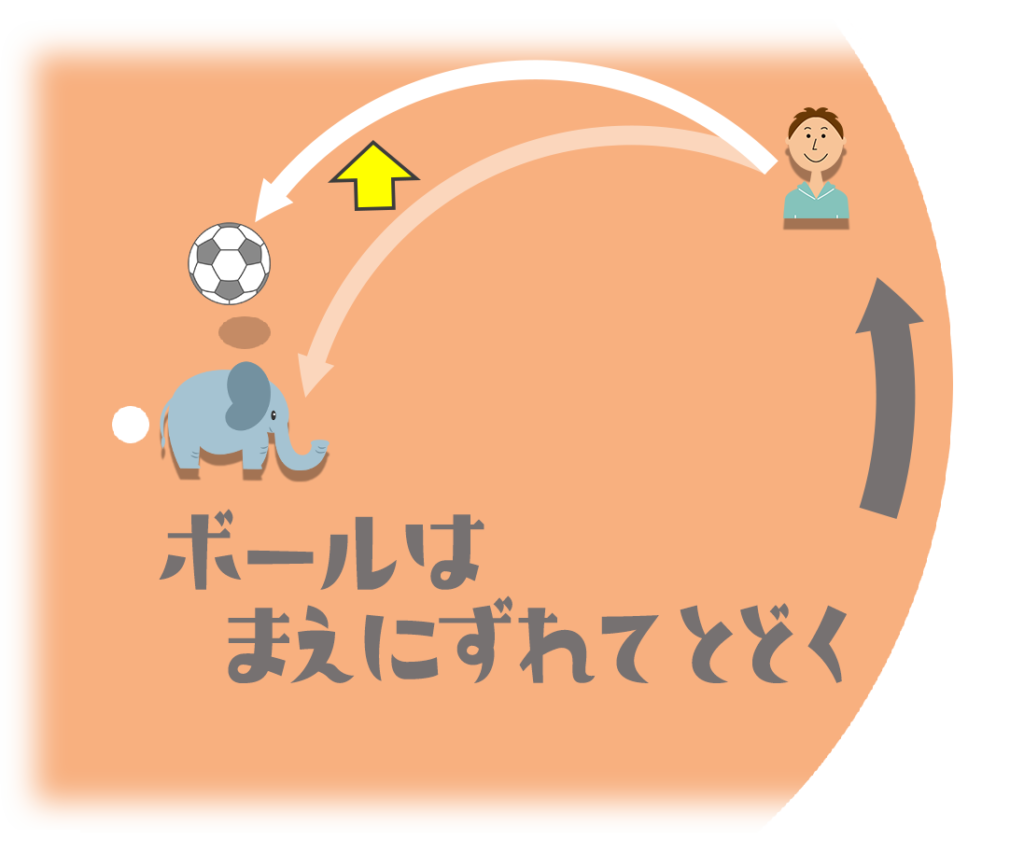
僕から見ればボールをゾウさんに向かって投げたはずなのに、ボールは右にずれてゾウさんの前の方に落ちちゃうんだ。
これを北半球で考えてみても同じようにボールは右にずれて飛んでいくよ。
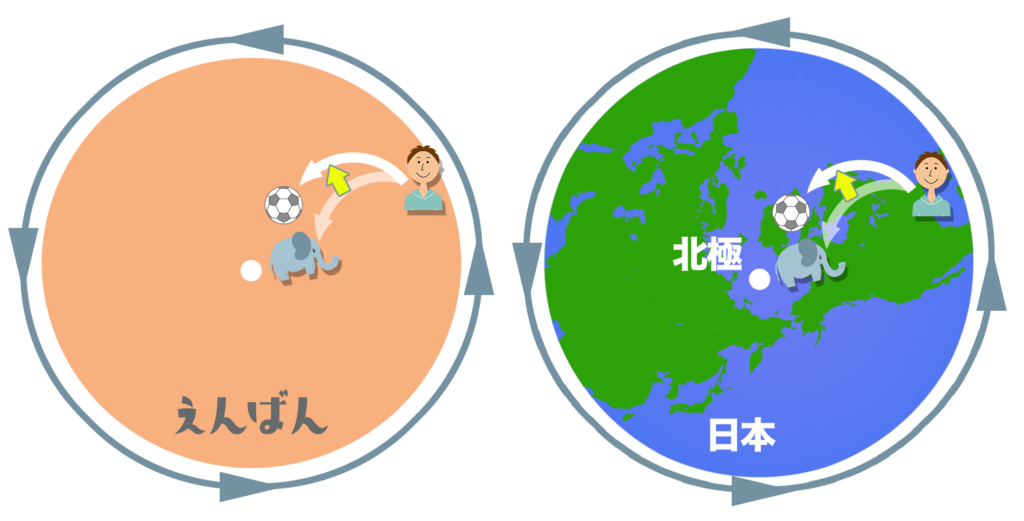
つまり北半球のどこでも「動いているものにはかならず右にずれるコリオリの力がはたらく」ってことなんだ。

へぇ〜、そういうことかぁ。
ところでコリオリって、人の名前なの?

そのとおり。
フランス生まれの天文学者、数学者、物理学者で、1820年〜1840年ごろにかけて活躍したんだ。そのころの日本は江戸時代。刀を持ったお侍(さむらい)さんがいたころだね。


南半球ではコリオリの力は左向きにかかるの?

そうだね。北半球と逆と考えればいいよ。
北半球に住んでいる人にとって地球の自転は左まわり。南半球に住んでいる人にとっては右まわり。だから南半球ではコリオリの力は左向きにものがずれる力になるんだ。
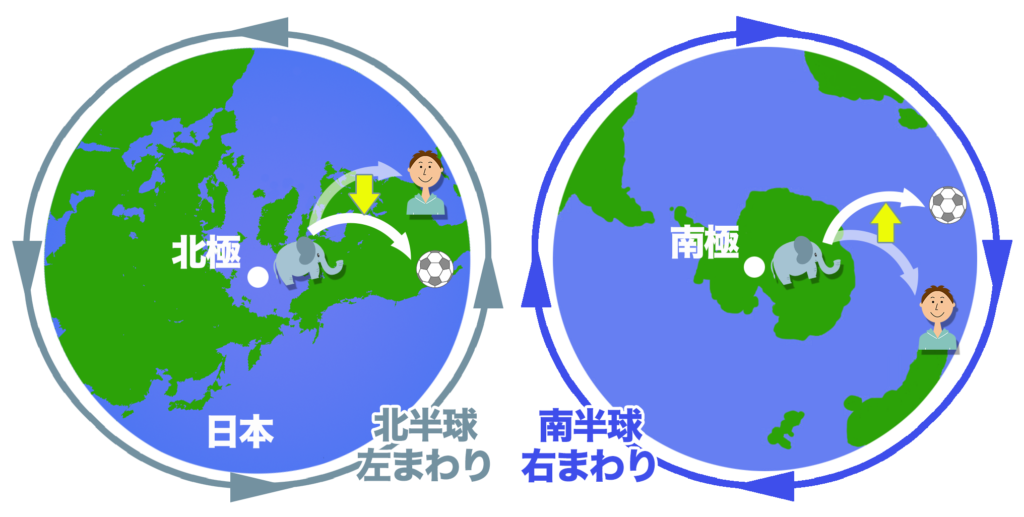

何だかごちゃごちゃしてきちゃったゾゥ

わかるわかる。
コリオリの力は北半球では右に、南半球では左に動かす力って覚(おぼ)えておけばいいよ。
ちなみに台風の風が左巻きなのは、もともと台風はまわりから空気を引き寄(よ)せる性質があって、空気は台風に向かいながらコリオリの力が働いて右にずれていくんだ。
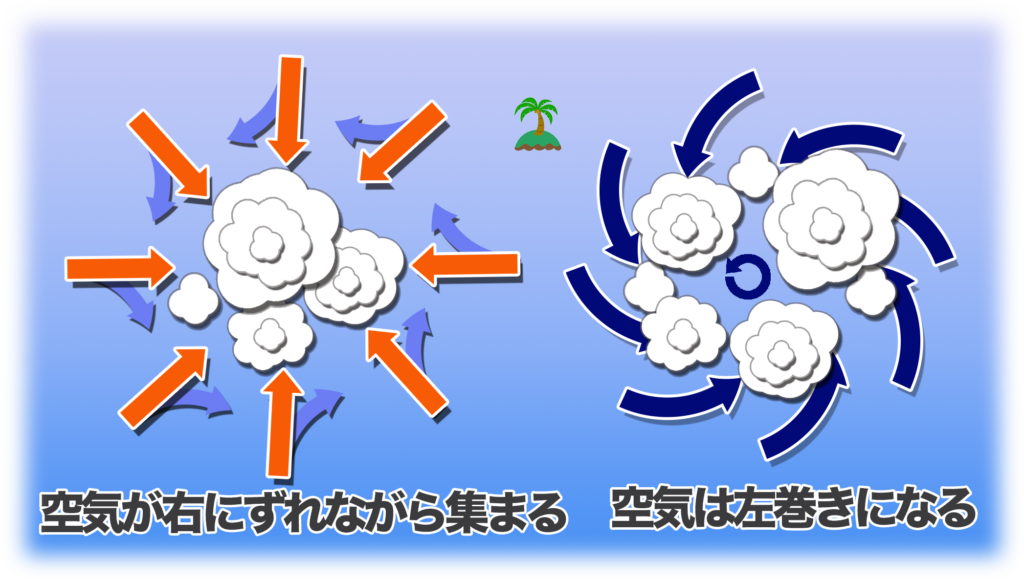
最終的に、空気は左巻きの風になって、台風の中心に向かっていくことになるんだよ。

そういうことかぁ



コメント